🔗 Istambul-BFT Consensus Algorithm

Thursday. May 22, 2025 - 40 mins

Istambul Byzantine Fault Tolerance

The Istanbul Byzantine Fault Tolerance (IBFT)a robust consensus algorithm vital for modern distributed systems, particularly in the realm of enterprise blockchains.The presentation covers how IBFT ensures reliability and consistency even in the presence of malicious or faulty nodes. I begin with a foundational understanding of Practical Byzantine Fault Tolerance (PBFT), a seminal algorithm from 1999 that laid much of the groundwork for BFT protocols. We will then transition to IBFT, exploring its core mechanisms, its ingenious adaptations for blockchain environments—especially its use of Proof of Authority—and how it addresses some of the challenges faced by its predecessors. By examining its normal operation, round change mechanisms, and critical justification logic, we will understand how IBFT achieves both safety and liveness. Finally, we’ll draw a concise comparison with other prominent BFT protocols, highlighting IBFT’s unique strengths in communication efficiency and immediate finality, making it an ideal choice for secure and high-performance permissioned networks.

Practical Byzantine Fault Tolerance (PBFT)

Practical Byzantine Fault Tolerance (PBFT), proposed by Barbara Liskov and Miguel Castro in 1999, aimed to make distributed systems reliable even in the presence of Byzantine faults. The core motivation was to achieve high availability and consistency in replicated systems. PBFT found practical application in servers, databases, financial services, and critical infrastructure. Its primary goal was to overcome the limitations of theoretical BFT algorithms, which were often inefficient for real-world use.

• A key immediate outcome of PBFT is that a decision is considered final after consensus is reached. This innovation has since inspired permissioned blockchains like Tendermint, IBFT, and HotStuff.

• While this discussion will focus on Istanbul Byzantine Fault Tolerance (IBFT), it’s important to understand PBFT first, as IBFT is heavily based on it. We’ll explore how PBFT works, and then discuss how IBFT differentiates itself and what new contributions it brought.

Motivation and Objectives of PBFT

PBFT was developed to ensure the reliability of distributed systems even when faced with Byzantine faults. Its practical applications include:

• Replicated servers: Such as databases and file systems.
• Critical infrastructures: Including financial systems and telecommunications.

The objective of PBFT was to create an efficient, Byzantine fault-tolerant algorithm that offered good performance and could be applied in practice, particularly in fault-tolerant replicated systems like banks and file systems. Although not originally designed for blockchains, this application emerged years later as permissioned blockchains began adapting it.

How PBFT Works

Like all BFT algorithms, PBFT achieves consensus through a majority vote among nodes. Correct nodes can effectively override the malicious behavior of Byzantine nodes.

Distributed systems can fail arbitrarily due to bugs, attacks, memory corruption, and so on. Byzantine Fault Tolerance (BFT) addresses these scenarios, but prior to PBFT, existing algorithms were too inefficient for practical use. PBFT was the first practical BFT protocol to offer good performance in real networks, with an acceptable communication cost of $O(n^2)$ at the time, and without requiring synchronized channels.

Advantages of PBFT

• Energy Efficiency: Since BFT protocols rely on voting among validators, they don’t require energy-intensive processes like mining or Proof of Work (PoW), significantly reducing computational and energy consumption.
• Transaction Finality: Unlike PoW, where multiple confirmations are often needed (and every node must individually verify all transactions before adding a new block to the blockchain), PBFT transactions achieve immediate finality, requiring no further confirmations.

PBFT Model and Phases

PBFT operates on a partially synchronous model, meaning that after an unknown global stabilization time (GST), there’s a known upper bound (Δ) on message delivery time.

It designates one node as the primary (leader), with all others acting as backups (secondaries). Any eligible node can become the leader. Each “view” has a sequential number and a designated leader, which rotates. The goal is for all honest nodes to reach consensus on the system’s state using a majority rule.

Normal Case

The normal case operation involves a three-phase consensus mechanism: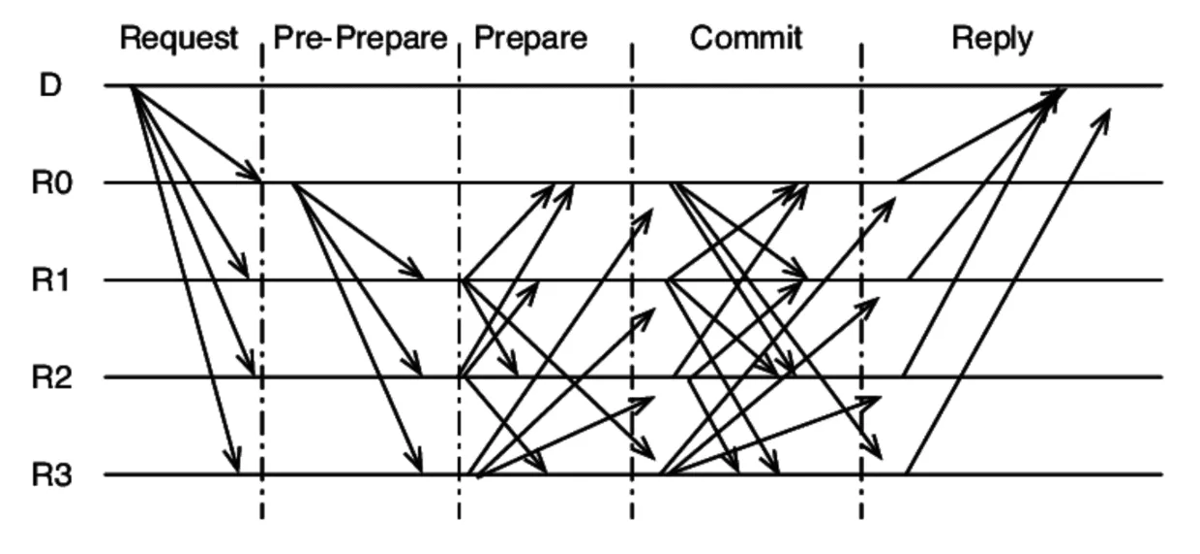

1. Pre-Prepare: The primary node (proposer) transmits a proposal to all other validators. These validators verify the validity and sequence number before proceeding to the Prepare phase.
2. Prepare: Upon receiving a valid proposal, validators send “prepare” messages to indicate their agreement on the proposed block. This phase essentially confirms that all nodes have a valid message. Validators wait to receive 2F+1 “prepare” messages from other validators before moving to the next phase.
3. Commit: Once a validator receives enough “prepare” messages, it sends a “commit” message to signal agreement on the proposed block.

Essentially: The primary node proposes (via pre-prepare messages) to all other nodes. Then, 2F+1 prepare and commit messages are exchanged before proceeding.

View Change Mechanism

A view change occurs when there’s suspicion of a failure or misbehavior by the current leader (primary). This is a recovery mechanism triggered only when the current leader is suspected of failing—for instance, if a timeout expires, the proposal is invalid, or the leader is slow. 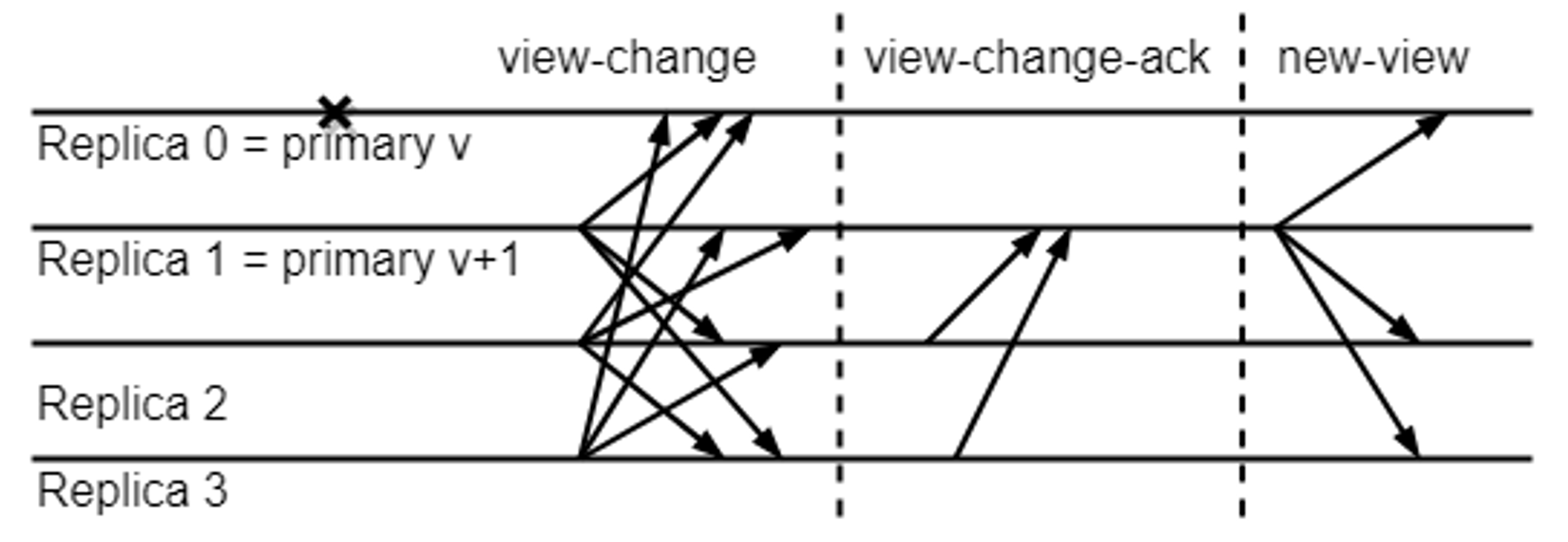Nodes issue VIEW-CHANGE messages to signal their desire to switch leaders. When a node receives enough view-change messages, it sends a confirmation message to the new prospective leader.

The new leader collects sufficient view-change messages (2F+1), assembles a consistent new state, and sends a NEW-VIEW message with a valid proposal. During a view change, the complexity is higher because a new leader must collect proofs (VIEW-CHANGE messages) from a quorum of validators and restart consensus with a NEW-VIEW.

Condition for safety: The maximum number of malicious nodes cannot be greater than or equal to one-third of all nodes in the system. Therefore, the more nodes in the system, the more secure it becomes.

Message Complexity

The message complexity differs between normal operation and view changes because nodes communicate and coordinate to ensure security and liveness in the presence of malicious nodes.

Normal Case: $O(n^2)$

• Pre-prepare: $O(n)$ (1 message from the leader to all n-1 replicas).
• Prepare: $O(n^2)$ (each node sends n-1 messages).
• Commit: $O(n^2)$.

  View Change: $O(n^3)$

• Nodes send VIEW-CHANGE messages to other nodes.
• Confirmation messages are sent to the new leader.
• If 2F+1 messages are received, the leader assembles a new state and sends a NEW-VIEW message with a valid proposal.
• The primary node collects $O(n)$ VIEW-CHANGEs, each containing $O(n)$ internal messages, resulting in $O(n^2)$ for collection.
• Broadcasting the NEW-VIEW message, which includes $O(n^2)$ (or 2F+1) content to n nodes, leads to a total complexity of $O(n^3)$.

Istanbul Byzantine Fault Tolerance (IBFT)

IBFT is a consensus mechanism inspired by PBFT (Practical Byzantine Fault Tolerance) and Clique Proof of Authority (PoA). Its primary motivation was to provide a suitable consensus algorithm for private, enterprise-grade blockchains.

IBFT is notably used in Besu, an Ethereum client developed by the Hyperledger project. Like PBFT, it operates with a requirement of 3F+1 nodes (validators) to tolerate Byzantine faults. A key differentiator is the selection of a new proposer for each round, with a mechanism called “Highest Prepared” being a significant addition. It leverages Proof of Authority (PoA) principles.

With the emergence of permissioned blockchains (such as Hyperledger Fabric, Quorum, Tendermint, etc.), developers began seeking alternatives to the Proof of Work (PoW) consensus model, which is often criticized for being expensive and slow.

IBFT and Hyperledger Besu

IBFT is one of the consensus algorithms employed by the Ethereum client Besu, developed as part of the Hyperledger project.

• Hyperledger: An open-source collaborative project hosted by the Linux Foundation, Hyperledger develops cross-industry blockchain technologies for enterprise use. Besu is one of its key components.
• Besu: An Ethereum client that implements the Ethereum protocol, allowing users to interact with the Ethereum blockchain. It is written in Java. Besu supports not only the public Ethereum network but also private and permissioned networks. It can be integrated with various consensus mechanisms, including PoW, IBFT, IBFT 2.0, Clique, and QBFT. This client can connect to the Ethereum network, validate blocks and transactions, create and interact with smart contracts, and provide APIs for developers and users.

IBFT specifically addresses some of the challenges encountered when attempting to use PBFT in a blockchain context.

Key Features and Mechanics of IBFT

• Fault Tolerance: To tolerate invalid nodes, the group of validators must consist of at least 3F+1 nodes.
• New Proposer Selection: A new proposer is selected for each round. This selection can occur via a round-robin approach or a sticky proposer mechanism (where the proposer only changes if a round-change event occurs). If a block fails to be inserted, the proposer changes, and the process restarts.
• State Replication: Each validator maintains a replica of the state to ensure block consensus.
• Block Locking (Implied): To ensure that only one block can be added to the state, IBFT prevents a proposed block from changing once a majority has agreed on its insertion. While not explicitly named “block locking” within IBFT’s description, this process serves the same purpose as ensuring the finality of a proposed block. Highest Prepared: During the consensus process, a pair of variables, pr and pv, are maintained. These are persisted and sent when a round change occurs. This mechanism helps ensure consistency across round changes.
• Proof of Authority (PoA): PoA is one of the mechanisms added to enable IBFT’s use in private and corporate environments. In a PoA system, only pre-approved and trusted validators can create new blocks. This is a crucial adaptation for enterprise blockchains where identities of validators are known and controlled.

Proof of Authority (PoA) Consensus Mechanism

Proof of Authority (PoA) is a consensus mechanism used by IBFT, offering a distinct approach compared to the more open participation models of Proof of Work (PoW) and Proof of Stake (PoS).

Core Characteristics of PoA

• Pre-Approved Validators: Only pre-approved validators are authorized to validate and decide on blocks. This signifies a limited and permissioned participation model.
• Known Identities: Unlike PoW or PoS where participants can be pseudonymous, in PoA, the identities of the validators are known. This means their reputation is at stake, providing a strong disincentive for malicious behavior. The entities responsible for the blockchain know exactly who the validators are, including their data, and only trusted individuals or companies are accepted. The guarantee of security comes from the low probability that validators would act maliciously, as everyone would know who did it.
• Predictable Block Intervals: New blocks are added at a predictable interval, making the network’s operation more consistent.
• Scalability and Performance: Due to a limited number of validators and no competitive mining process, PoA-based systems are generally more scalable, exhibit higher performance, and have lower energy consumption compared to PoW. They achieve high throughput because fewer validators mean faster coordination, and there’s no competition involved (no mining).
• Low Energy Consumption: PoA does not require intensive computational power (like PoW) or significant token allocation as collateral (like PoS). Instead, the “stake” for validators is their identity and reputation.
• Ideal for Private/Enterprise Blockchains: Being a permissioned system, PoA is ideally suited for private and enterprise blockchains where trust is established among known participants and the focus is on security and speed.

How PoA Functions in IBFT

• Validator Selection: The right to generate new blocks is granted exclusively to these pre-approved nodes, which are referred to as “Validators.”
• Leader Rotation: The choice of the leader (proposer) typically follows a round-robin rotation.
• Automated Block Decision: Validators collectively decide whether a new block will be added or not through an automated process. They run the blockchain client, which allows them to propose and validate transactions and blocks, verifying the digital signatures associated with each message.
• Permissioning: Permission to be a validator is typically granted by the owning team or enterprise operating the blockchain.

Security Considerations in PoA

While PoA offers advantages in performance and governance, it’s crucial to consider its security implications:

• Centralization Trade-off: PoA inherently involves less decentralization compared to public, permissionless blockchains using PoW or PoS, as participation is restricted.
• Vulnerability to Malicious Actors/Compromise: Any system can be affected if its participants act maliciously or if their systems are compromised.

Common Attack Vectors and PoA’s Resilience:

• DDoS (Distributed Denial of Service) Attacks: An attacker sends a large number of transactions or blocks to a node with the intention of making it unavailable. PoA networks, due to their limited validator set, might have specific mitigation strategies, though DDoS can still be a general threat to any network.
• 51% Attack: This attack typically refers to gaining control of 51% of the network’s computational power (PoW) or staked tokens (PoS). In PoA, an equivalent would be a Group Attack, where it would require 51% of the validators within the blockchain (who are typically from different organizations or locations) to conspire to influence decisions. This is significantly harder to achieve than in open networks, given the known identities and reputational risk.

Validator Management

The set of validator nodes can be renewed or modified as needed, allowing the network operators to manage the trusted participants.

Best Use Case

PoA is best suited for private, enterprise blockchains that prioritize security and speed over maximum decentralization, where trust among known participants is a foundational element.

Correctness Properties of IBFT

Like any Byzantine Fault Tolerant (BFT) algorithm, IBFT must guarantee three fundamental properties to ensure the integrity and progress of the system. These are often referred to as “preliminaries” by the authors of relevant papers, signifying the foundational assurances of why and how the algorithm ensures that correct nodes make secure and valid decisions.

1. Agreement (Consistency)
   • Definition: “If a correct process decides on a value v, then no other correct process decides on a different value.”
   • Significance: This property guarantees safety. It ensures that the network does not split, meaning there won’t be different blocks at the same height (or state) across correct nodes. Even in the presence of Byzantine nodes, honest nodes will never conflict on which block has been decided.
2. Validity (External Validity)
   • Definition: “If a correct process decides on a value v, then $\beta(v)$ is true.”
   • Significance: This is where the function $\beta$ (beta) comes into play. $\beta$ is an external predicate provided by the application itself (e.g., a blockchain) to verify if the value being decided is valid within the system’s context.
     • IBFT does not define what constitutes a valid value; instead, it delegates this responsibility to the application through the $\beta$ function.
     • For example, in a blockchain context, the consensus mechanism needs to accept only blocks containing legitimate transactions. The predicate $\beta$ prevents blocks with false or duplicated transactions from being considered valid. This makes IBFT flexible and secure, as the application can define its own rules for validity.
3. Termination (Liveness)
   • Definition: “Every correct process eventually decides.”
   • Significance: This property ensures liveness. It guarantees that the IBFT protocol does not get stuck indefinitely. Even with failures present in the network, the algorithm ensures that correct processes will eventually reach a decision and continue processing.

In essence, IBFT ensures all correct processes agree on the same value(agreement), the agreed-upon value is valid according to the application’s logic (e.g., a valid block) and all correct processes eventually reach a decision. These properties collectively explain why and how IBFT ensures that correct nodes make secure and valid decisions, even in the face of Byzantine faults.

Consensus Mechanism and Phases

IBFT employs a three-phase consensus mechanism similar to PBFT:

• Pre-Prepare: The designated proposer broadcasts the proposed block to all validators.
• Prepare: Validators confirm receipt and agreement on the proposed block.
• Commit: Validators confirm their final agreement to accept the block.

These phases are part of the core process that looks like this: Propose → Pre-Prepare → Prepare → Commit.

Guarantees and Quorum Rules

• Safety and Liveness: IBFT guarantees both safety (all correct nodes agree on the same value) and liveness (all correct nodes eventually reach a decision).
• Fault Tolerance: The system is designed to tolerate up to $f$ Byzantine faults. To ensure security and consensus, the total number of nodes $(n)$ must satisfy the condition: $n≥3f+1$. This means that even with up to f faulty nodes, there are still at least $2f+1$ correct processes, which is sufficient to ensure consensus among honest participants.
• Quorum: Consensus is achieved when a quorum of $2f+1$ validators agree on a decision.

Message Complexity and Latency

• Message Complexity: IBFT maintains an $O(n^2)$ message complexity in both normal operation and during a round change. This is a key difference from PBFT, which had an $O(n^3)$ complexity during view changes. This improvement contributes to IBFT’s suitability for enterprise blockchains.
• Message Delays/Latency: The core consensus process typically involves 3 communication steps (corresponding to the three phases), contributing to predictable latency.

System Model of IBFT

The system model outlines the fundamental assumptions about the environment in which IBFT operates, including how processes (nodes) behave, how they communicate, and what types of failures can occur.

Process States

Each process (or node) within the system can be in one of two states:

• Correct: These processes strictly follow the algorithm as it’s defined.
• Faulty (Byzantine): These processes can behave arbitrarily. They might lie, send incorrect messages, ignore messages, or act maliciously in any way.

Fault Tolerance

As mentioned, IBFT is designed to tolerate up to f Byzantine processes. The crucial condition n≥3f+1 ensures that even with f faulty processes, the remaining $2f+1$ correct processes can always reach consensus.

Communication Model

• Broadcast Communication: Every process can send a message to all other processes in the set $\Pi={p1,p2,…,pn}$, including itself. This simplifies the algorithm by ensuring that, in theory, everyone receives the same information.

Time Model

• Partially Synchronous System: The system is considered partially synchronous.
• Before the Global Stabilization Time (GST): Messages can be arbitrarily delayed or lost.
• After the GST: The system behaves predictably. Any message sent by a correct process at time $t \ge GST$ will be delivered to all other correct processes by $t + \Delta$, where $\Delta$ is a fixed, known time bound. This ensures that eventually, messages are delivered reliably and within a predictable timeframe, allowing the protocol to make progress.

IBFT Flow

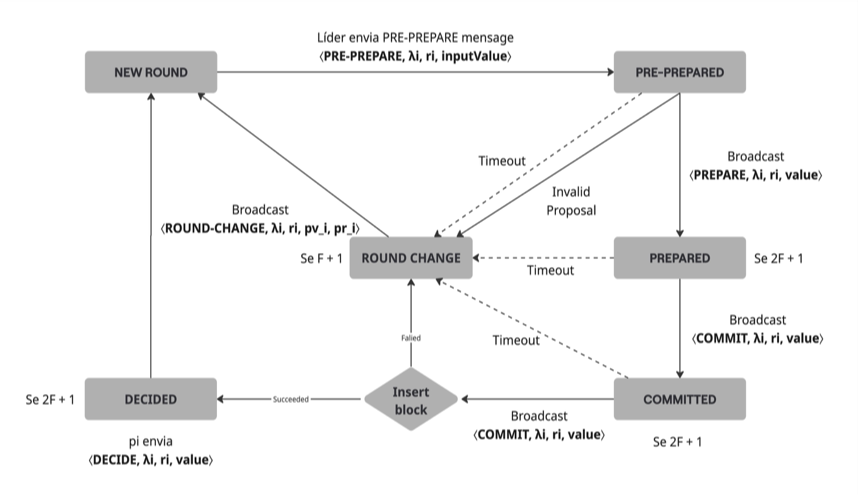
Normal Consensus Flow

The IBFT consensus proceeds through a series of steps involving the Proposer (the current leader) and the Validators (all other participating nodes):

• Proposer Collects Transactions: The designated Proposer for the current round gathers a set of transactions from its transaction pool.
• Proposer Generates and Broadcasts Block Proposal (Pre-Prepare): The Proposer then assembles these transactions into a candidate block and generates a block proposal. It sends this proposal to all other Validators. Upon sending this message, the Proposer enters the PRE-PREPARED state.
• Validators Enter Pre-Prepared State: Each Validator, upon receiving a valid PRE-PREPARE message from the Proposer, also transitions into the PRE-PREPARED state.
• Validators Broadcast Prepare Messages: After entering the PRE-PREPARED state and verifying the proposal, each Validator sends a PREPARE message to all other Validators (including the Proposer).
• Validators Enter Prepared State: Each Validator, upon receiving $2F+1$ valid PREPARE messages (including its own), transitions into the PREPARED state. This indicates that a sufficient number of validators have agreed on the block’s validity and content.
• Validators Broadcast Commit Messages: Once in the PREPARED state, each Validator sends a COMMIT message to all other Validators.
• Validators Enter Committed State: Each Validator, upon receiving $2F+1$ valid COMMIT messages (including its own), transitions into the COMMITTED state. This signifies that the block has been finalized by a supermajority.
• Validator Attempts Block Insertion (Decided): A Validator then attempts to insert the committed block into its local blockchain. If the insertion is successful and valid, the Validator enters the DECIDED state, confirming the block has been added to the chain.
• New Round/Timer Initiation: After a block is successfully decided, Validators can then choose a new Proposer and initiate a new round, often with a new timer.

Round-Change Mechanism

A Round-Change mechanism is crucial for liveness and occurs when the consensus process gets stuck or faces issues. This typically happens if:

• A timeout occurs (the current round takes too long).
• The proposal is found to be invalid.
• The block insertion fails after commitment.

When any of these conditions are met:

• Round-Change Messages: Validators who detect a problem will send ROUND-CHANGE messages to signal their intent to move to a new round with a different proposer.
• Proposer Selection for New Round: Upon receiving $F+1$ ROUND-CHANGE messages, a new Proposer is selected for the next round. If this new Proposer already has cached pv (prepared value) and pr (prepared round) values from a previous successful PREPARE phase, these values are used to ensure consistency. Otherwise, the new round starts with a fresh proposal.
• New Round Initiation: The new Proposer then initiates a new round using these determined values.

In the context of Besu, the Ethereum client that implements IBFT 2.0, the inputValue isn’t just a single transaction. Instead, it represents the candidate block of transactions that a validator would like to see included in the blockchain.

Specifically, this inputValue is a complete and valid Ethereum block, similar to the type of block that would be mined in a Proof of Work system. It includes:

• A set of transactions from the validator’s transaction pool.
• A block header that is compatible with the current state of the chain.
• extraData containing the digital signatures of the validators who have approved the block.
• Standard block metadata like the block number, parent block hash, and so on.

This block is entirely assembled by the leader (proposer) from their inputValue. This means that each validator holds its own inputValue—the block it would propose if it were the leader of the round.

Instances and Rounds

In IBFT, each instance $\lambda$ of the algorithm represents a single attempt to reach consensus—for example, deciding on the next block in a blockchain. This process is executed in rounds.

• Within each round, there’s a designated leader (proposer) whose role is to propose a value (e.g., a new block).
• The selection of this leader for each round is determined by a deterministic function leader(λ, round). This function is designed to ensure that at least f+1 different nodes will serve as leaders across various rounds, preventing any single node from monopolizing the leadership role.

Message Types

IBFT relies on four primary types of messages to coordinate consensus among nodes:

1. $⟨PRE-PREPARE,λ,r,value⟩$: Sent by the leader to broadcast a proposed value for a given instance $\lambda$ and round $r$.
2. $⟨PREPARE,λ,r,value⟩$: Sent by validators to indicate their agreement with the proposed value after initial validation.
3. $⟨COMMIT,λ,r,value⟩$: Sent by validators to confirm their final decision to accept the value.
4. $⟨ROUND-CHANGE,λ,r,pr,pv⟩$: This message is crucial for fault recovery. It’s used when the current leader is suspected of failing or communication is slow.
   • It contains the previous prepared round $(p_r)$ and the prepared value $(p_v)$ from that round. This information is vital for ensuring safety and consistency even after a leader change, allowing the new leader to build upon the last agreed-upon state.

Local State Variables for Each Process $p_i$

Every process (node) $p_i$ maintains several key local state variables:

• $\lambda_i$: The instance number. In a blockchain context, this typically corresponds to the block height. This value remains constant throughout a consensus attempt for a particular block.
• $r_i$: The current round for process $p_i$. This usually starts at 1 and increments if round changes occur.
• $pr_i,pv_i$: These store the last round (pr for “prepared round”) in which $p_i$ was prepared, and the corresponding value (pv for “prepared value”) that was prepared in that round. If $p_i$ hasn’t been prepared yet in any round, these values are initialized to $\perp$.
• $inputValue_i$: The value that $p_i$ itself would like to propose if it were the leader. As we discussed, for Besu, this would be a complete, valid Ethereum block.

Timer Mechanism

Each process $p_i$ also has a timer, $timer_i$, which plays a vital role in ensuring liveness:

• The timer is activated and, if consensus takes too long, it triggers a round-change mechanism.
• Crucially, the waiting time increases exponentially with the round number $(t(r_i))$. This exponential backoff helps prevent premature round changes that could destabilize the network, while still ensuring progress if a genuine issue arises.
• When $timer_i$ expires, it automatically triggers the sending of a ⟨ROUND-CHANGE⟩ message.

Normal Case Operation

The logic of the IBFT algorithm is defined by event-driven rules, often referred to as “upon” rules. These rules specify actions to be taken when certain conditions are met, typically upon receiving specific messages or detecting a state change.

For example, a rule might state: “Upon receiving $⌊(n+f)/2⌋+1$ PREPARE messages with the same value in the current round, then execute action X.” These rules are generally triggered at most once per round for specific state transitions, though some final decision rules might be activated multiple times if valid quorums are achieved.

Step 1: PRE-PREPARE (Leader Proposes)

• A process $p_i$ initiates the execution of an instance $\lambda$ by calling $START(λ, inputValue)$. This typically happens when it’s time to propose a new block (e.g., at a new block height).
• If $p_i$ is the $leader(\lambda, r_i)$ for the current round $r_i$:
  • It sends a broadcast message: $⟨PRE-PREPARE,\lambda_i,r_i, inputValue⟩$. This action signifies the leader’s proposal for the value (e.g., the next block) to be agreed upon in this round.

    Step 2: PREPARE (Processes Accept Leader’s Proposal)

• Upon receiving a $⟨PRE-PREPARE,\lambda,r,value⟩$ message from the designated $leader(\lambda, r)$:
  • The process $p_i$ first checks if the message is valid (e.g., correct signatures, sequence numbers).
  • It then verifies if the proposal is justified by calling $JustifyPrePrepare(m)$. This function ensures the proposal aligns with system rules and any previously prepared state (especially important during round changes, though in the normal case, it might simply check for a fresh proposal).
• If both conditions are met:
  • Process $p_i$ restarts its timer $(timer_i)$. This fresh start ensures that a round-change is only triggered if progress genuinely stalls.
  • Process $p_i$ sends a broadcast message: $⟨PREPARE,\lambda_i, r_i, value⟩$. This signals its agreement with the leader’s proposal to all other processes.

    Step 3: COMMIT (Confirmation that the Block Will Be Accepted)

• Upon receiving a quorum of valid $⟨PREPARE,\lambda_i, r_i,value⟩$ messages (from at least $⌊(n+f)/2⌋+1$ processes, all with the same value for the current round $r_i$):
  • Process $p_i$ updates its local state variables:
    • $pr_i←r_i$ (records the current round as the last prepared round).
    • $pv_i←value$ (records the agreed-upon value as the last prepared value).
  • Process $p_i$ sends a broadcast message: $⟨COMMIT,\lambda_i,r_i,value⟩$. This final confirmation signals its readiness to commit the block.

    Step 4: DECIDE (Final Agreement)

    Upon receiving a quorum of valid $⟨COMMIT,lambda_i,r_i,value⟩$ messages (from at least $⌊(n+f)/2⌋+1$ processes, all with the same value): Process $p_i$ stops its timer $(timer_i \leftarrow \text{stopped})$. Process $p_i$ executes: $Decide(\lambda_i, value, Q_commit)$. This is the point where the process finalizes the decision for instance $\lambda_i$ with the value (e.g., adds the block to its chain). $Q_commit$ might represent the set of commit messages forming the quorum, serving as a proof of finality.

Validations and Security

The security and correctness of this normal operation depend critically on:

• Quorums: Ensuring that a sufficient number of PREPARE and COMMIT messages (at least $2f+1$ or $⌊(n+f)/2⌋+1$ processes, given $n=3f+1$) are received before transitioning to the next phase. This majority ensures that even if f nodes are Byzantine, the correct nodes still outnumber them.
• Digital Signatures: All messages are digitally signed, ensuring their authenticity (they truly came from the claimed sender) and integrity (they haven’t been tampered with).
• External Validity Verification $(\beta)$: The $\beta(\text{value})$ function (as discussed in the correctness properties) is implicitly checked at various stages (e.g., when receiving a PRE-PREPARE or before sending a PREPARE message). This prevents the acceptance of blocks with invalid transactions or states, providing external consistency.

Pseudocode for Round Changes

This section of the pseudocode details how IBFT handles round changes. This mechanism is crucial for ensuring liveness—that is, the system’s ability to continue making progress even when the current leader is slow or malicious, or when the consensus instance gets stuck.

Step 1: Timer Expiration → Initiating a Round Change

The round change process is primarily triggered by a timeout.

• When timer_i expires for process $p_i$:
  • Process $p_i$ increments its current round number for this instance: $r_i\leftarrow r_i+1$.
  • It restarts its timer_i with the new, potentially exponentially increased, timeout value.
  • It then broadcasts a ⟨ROUND-CHANGE,\lambda_i,r_i,pr_i,pv_i⟩$ message. This message signals to other processes that $p_i$ suspects a stall and wishes to move to a new round. The inclusion of $pr_i$ and $pv_i$ (the last prepared round and value) is vital for maintaining safety during the transition.

Step 2: Receiving f+1 Round-Change Messages

A process $p_i$ doesn’t just act on its own timer; it also reacts to the collective signaling of other processes.

• If $p_i$ receives $f+1$ (or more) $⟨ROUND-CHANGE⟩$ messages where the round number $(r_j)$ in those messages is greater than its own current round $r_i$:
  • It identifies the smallest r_min among the received ROUND-CHANGE messages. This helps ensure that all honest nodes try to converge on the same new round.
  • It updates its own current round: $r_i\leftarrow r_min$.
  • It restarts its $timer_i$ and immediately broadcasts a new $⟨ROUND-CHANGE \lambda_i,r_i,pr_i,pv_i⟩$ message, reflecting its updated local round and its current prepared state $(pr_i, pv_i)$.

Step 3: New Leader Collects Quorum and Proposes Value

This step describes the behavior of the new leader that takes over after a round change.

• When the new leader (determined by the $leader(\lambda_i, r_i)$ function, which now identifies $p_i$) receives a quorum of valid $⟨ROUND-CHANGE⟩$ messages (from at least $2f+1$ processes) and these messages are justified:
  • The leader first checks if there’s a previously prepared value across the received quorum. This is done by a function like HighestPrepared(Q_rc). This function would look for the highest pv (prepared value) associated with the highest pr (prepared round) among the valid ROUND-CHANGE messages in the quorum $Q_rc$.
  • If $HighestPrepared(Q_rc)$ is not $\perp$ (meaning a value was previously prepared by a supermajority):
    • The new leader proposes this value $(v)$. This is critical for safety, ensuring that if a previous round already reached the PREPARED state for a specific value, that value is maintained.
  • Otherwise (if no value was previously prepared by a supermajority, or HighestPrepared returns $\perp$):
    • The new leader proposes its own $inputValue_i$ (the value it initially intended to propose for this instance, from the Start call). This effectively starts the consensus on a fresh proposal.
  • Finally, the new leader sends a $⟨PRE-PREPARE,\lambda_i,r_i,v⟩$ message, signaling the beginning of a new attempt at consensus in the new round.
• From this point onward, the execution continues as described in Algorithm 2 (Normal Case Operation). The new leader’s PRE-PREPARE message kicks off the standard three-phase consensus flow (PRE-PREPARE, PREPARE, COMMIT) in the new round.

Pseudocode for Message Justification

This final part of the pseudocode is critical for how IBFT ensures both liveness (the system keeps making progress) and safety (decisions are never contradictory or overwritten), especially when round changes occur. It focuses on message justification.

Objective: Safety Across Rounds

The primary objective of message justification is to guarantee that a value that has already been “prepared” (and thus potentially “decided”) cannot be overwritten by a different value in a subsequent round.

This is based on a core Safety Principle (Safety across rounds): If a value v could have been decided in round $r$, then only $v$ can be proposed in any subsequent round $r’>r$. To uphold this principle, leaders and processes follow specific justification logic that analyzes prepared values from earlier rounds.

Justification Functions:

1. $JustifyRoundChange(Q_rc)$
   • This function receives a quorum $Q_rc$ of ⟨ROUND-CHANGE⟩ messages. It returns true if one of the following conditions is met:
     • J1: All messages in $Q_rc$ have $pr=\perp$ and $pv=\perp$ (meaning no one in the quorum has prepared any value yet for this instance in a previous round); OR
     • J2: There is a quorum of ⟨PREPARE⟩ messages that justifies the highest $(pr,pv)$ pair among the messages in $Q_rc$. This condition confirms that the highest prepared value seen is indeed reliable and was agreed upon by a supermajority.
2. $JustifyPrePrepare(m)$
   • This function checks whether a proposal sent by a leader (a $⟨PRE-PREPARE,\lambda_i,round,value⟩$ message $m$) is safe. It returns true if:
     • The current round is the first round (round 1), meaning no prior rounds or justifications are needed; OR
     • There exists a quorum $Q_rc$ of $⟨ROUND-CHANGE⟩$ messages (collected by the new leader) that satisfies either:
   • J1 (No one prepared yet): No one in the quorum has a prepared value $(pr=⊥∧pv=⊥)$; OR
   • J2 (Highest prepared matches proposed value): A specific value $(value)$ is the highest prepared value $(pr,value)$ according to $HighestPrepared(Q_rc)$, and this value is precisely the one being proposed in the ⟨PRE-PREPARE⟩ message.
3. $HighestPrepared(Q_rc)$
   • This is an auxiliary function that analyzes a quorum $Q_rc$ of ⟨ROUND-CHANGE⟩ messages. Its purpose is to find the pair $(pr,pv)$ with the highest round number $(pr)$ among those messages, provided that this pair is indeed justified by a quorum of ⟨PREPARE⟩ messages. This function effectively identifies the most “committed” value from previous rounds across the quorum.

Motivation Behind Justification

The primary motivation for these justification rules is to ensure that even with round changes guaranteeing liveness, the system’s safety is never compromised. We must prevent a situation where a value is decided and then later overwritten by a different, contradictory value.

Example: If a value $v$ was PREPARED in round 2 by $f+1$ processes (a sufficient number to potentially lead to a decision), then any subsequent quorum of ⟨ROUND-CHANGE⟩ messages will necessarily contain at least one honest process that has prepared this value $v$. The HighestPrepared function would identify this $v$. Consequently, the new leader for a subsequent round would be obligated to propose $v$ again due to the JustifyPrePrepare rule. This ensures that there is no risk of a new, different value $v′\ne v$ being proposed and ultimately decided.

Handling Malicious Behavior:

• Malicious Leader: If a malicious leader attempts to propose an incorrect value in a new round, honest processes will reject it via the JustifyPrePrepare function because the proposed value won’t match the HighestPrepared value from the collected ⟨ROUND-CHANGE⟩ quorum.
• Malicious Process Lying about $pr$ and $pv$: If a faulty process lies about its pr or pv values in its ⟨ROUND-CHANGE⟩ message, its message will be effectively ignored by JustifyRoundChange and HighestPrepared. This is because the lying process won’t be able to provide the necessary quorum of PREPARE messages to justify its fabricated pr and pv values, thus failing the justification check.

In summary:

• JustifyRoundChange: Only allows round changes that are based on verifiable facts from a quorum.
• JustifyPrePrepare: Ensures that only safe and consistent proposals from the new leader are accepted.
• HighestPrepared: Accurately determines the most secure and previously agreed-upon value to be proposed in a new round.

Comparison with Other BFT Protocols

Now, let’s compare IBFT with other Byzantine Fault Tolerant protocols, focusing on latency and communication complexity.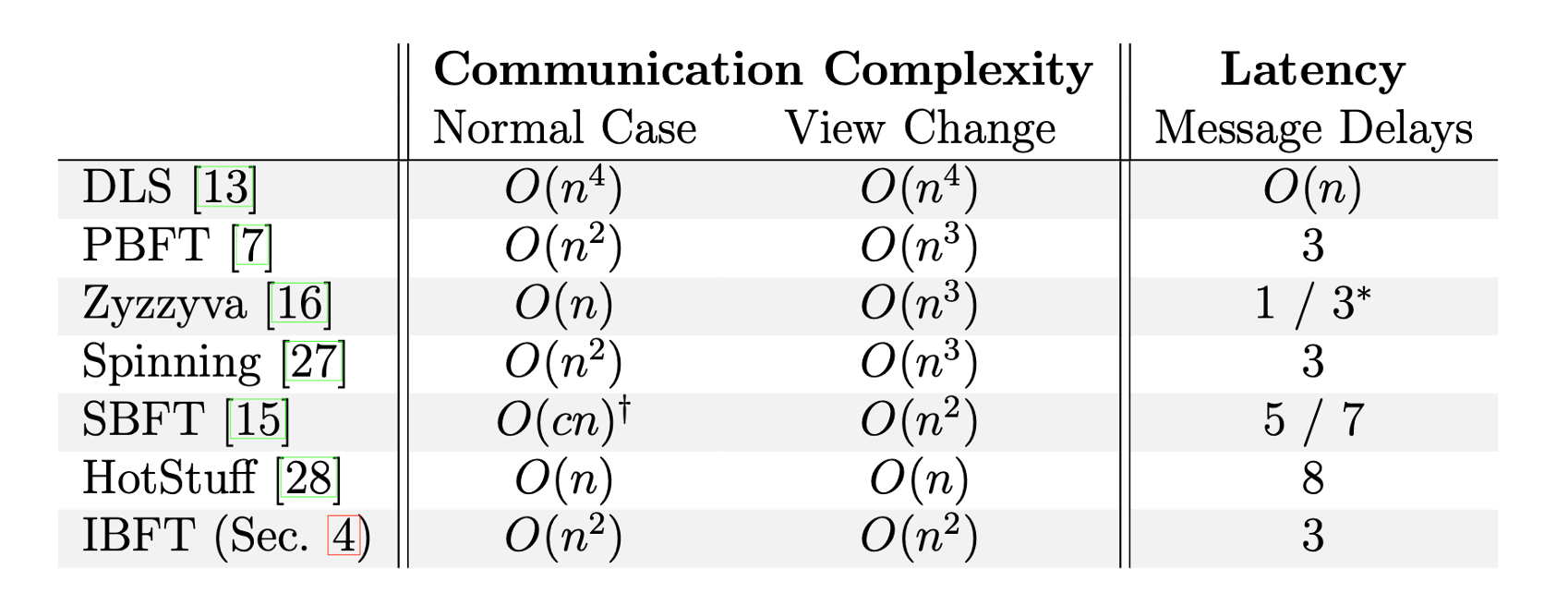

IBFT’s Key Advantages:

IBFT aims to achieve the same low latency as protocols like PBFT, Zyzzyva, and Spinning, but with a significant improvement in communication complexity, particularly during fault recovery scenarios.

Communication Complexity

• Normal Case: $O(n^2)$
  • In the normal case, during the PREPARE and COMMIT phases, each node sends messages to all other $n$ nodes (including itself). With $n$ nodes doing this, the total number of messages exchanged is $O(n^2)$.
• This is identical to PBFT in its normal operation.
• Round Change / View Change (Worst Case): This is where IBFT differentiates itself significantly from PBFT.
  • PBFT (Worst Case: $O(n^3)$)
    • During a VIEW-CHANGE, each replica sends a VIEW-CHANGE message to the new leader.
    • The new leader collects n - f of these messages.
    • Crucially, each VIEW-CHANGE message includes a set of all previously received PREPARE messages by the sender for that instance. Since a process might have received up to $O(n)$ PREPARE messages (e.g., $2f$ PREPARE), the new leader needs to process up to $O(n^2)$ messages just to reconstruct the state from the collected VIEW-CHANGE messages.
    • After reconstructing the state, the leader broadcasts a NEW-VIEW message containing all this consolidated information to all $n$ nodes.
    • Resulting Complexity:
      • Sending VIEW-CHANGEs: $O(n)$ VIEW-CHANGE messages, each potentially containing $O(n)$ internal messages, leading to $O(n^2)$ just for the collection phase.
      • Broadcasting NEW-VIEW: Broadcasting a NEW-VIEW message with $O(n^2)$ content to n nodes results in a total complexity of $O(n^3)$ in the worst case.
  • IBFT (Worst Case: $O(n^2)$)
    • IBFT optimizes the round change process with two key modifications:
      1. Summarized Justification: Each validator sends only one ROUND-CHANGE message. This message contains at most one justification (the HighestPrepared information). This justification is proof that progress was made in a previous round.
      2. No Full History: These justifications do not carry multiple state messages like PBFT’s PREPAREs. Instead, they typically contain only a hash and a certificate (e.g., a digest of the block along with the $2f+1$ PREPAREs that justify it).
      3. Optimized Leader Processing: The new proposer (leader) does not need to process all previous state messages from all nodes. It only needs to process the most recent justified information with the highest prepared value ($pv$).
    • Resulting Complexity:
      • Each validator sends an $O(1)$ ROUND-CHANGE message, which has a content size of $O(n)$ (due to potentially including a certificate that refers to other n nodes).
      • Broadcasting these messages to all n nodes results in a total complexity of $O(n^2)$.

Latency (Message Delays)

• IBFT vs. PBFT: IBFT maintains the same low latency (3 message delays) as PBFT. These 3 delays correspond to the three communication phases (PRE-PREPARE, PREPARE, COMMIT) within a single view/round.
• Comparison to HotStuff: HotStuff is a more recent BFT protocol that boasts linear communication complexity ($O(n)$). However, it typically achieves this at the cost of higher latency. The comment about “higher latency” might refer to the number of sequential communication steps or phases required for finality, which in some HotStuff variants can be more than 3 per decision. (Note: The specific context and variant of HotStuff are important here, as different interpretations or implementations might have varying latency characteristics).

In summary, IBFT provides a significant improvement over PBFT by maintaining the same low latency during normal operation while drastically reducing the worst-case communication complexity during fault recovery (round changes) from $O(n^3)$ to $O(n^2)$. This makes IBFT particularly well-suited for permissioned blockchain environments where efficiency and predictability are paramount.

IBFT Adaptation	Why It Was Made (Motivation)	How It Was Implemented
1. Proof of Authority (PoA) & Fixed Validator Set	In permissioned blockchains, not everyone can propose blocks. There’s a need for a controlled environment where participants are known and trusted.	IBFT leverages a known and defined set of validators, typically specified via a PoA contract or configuration. This contrasts with the dynamic, less controlled validator sets in more open BFT contexts.
2. Blocks as the Object of Consensus	Traditional BFT often focuses on agreeing on simple operations or arbitrary values. Blockchains, however, need to agree on entire blocks, which are complex data structures containing multiple transactions, a header, and hashes.	In IBFT, proposals and commits explicitly refer to complete blockchain blocks, including their transactions (txs), header information, and cryptographic hashes. This is a direct adaptation to the blockchain data model.
3. Digital Signatures on Blocks (vs. MACs)	PBFT often uses Message Authentication Codes (MACs) for authenticity. However, MACs are inefficient and not scalable for public-facing blockchains or large validator sets, as they require shared secrets or pairwise authentication.	IBFT employs digital signatures, typically ECDSA (Elliptic Curve Digital Signature Algorithm), which are standard in blockchain environments. These signatures are often aggregated or included in the extraData field of the block header, providing efficient and verifiable authentication without shared secrets.
4. Immediate Finality (No Forks)	Blockchains, especially in enterprise contexts, often require deterministic consensus without the possibility of “reorganizations” (forks) that can occur in probabilistic finality mechanisms (like PoW).	In IBFT, a block is considered finalized after it receives 2f+1 COMMIT messages. Once committed by this supermajority, there is no possibility of the block being reversed or replaced, providing strong, immediate finality.
5. Optimized Round Change with Justification	To guarantee network liveness and ensure progress, even when proposers are malicious or slow, an efficient recovery mechanism is needed without compromising safety. PBFT’s view change could be very heavy.	IBFT implements a more efficient round change mechanism using the HighestPrepared function and view justification. This avoids the $O(n^3)$ complexity of PBFT’s view changes by ensuring that ROUND-CHANGE messages only carry summarized proof of progress (e.g., a hash and certificate for the highest prepared value) rather than full message histories. This optimizes communication during leader failures.

Conclusion

In conclusion, we have traversed the landscape of Byzantine Fault Tolerance, from the pioneering PBFT to the adapted and optimized IBFT. We’ve seen how PBFT provided the foundational principles for achieving consensus in the face of arbitrary node failures, laying the groundwork for practical BFT implementations. IBFT, building upon this legacy, cleverly integrates Proof of Authority (PoA) and refines the consensus process to meet the specific demands of private, enterprise-grade blockchains.

Its ability to treat full blocks as the object of consensus, leverage efficient digital signatures, and guarantee immediate finality without forks positions it as a highly suitable choice for critical applications. Furthermore, IBFT’s innovative round-change mechanism significantly improves upon PBFT’s worst-case communication complexity, achieving an $O(n^2)$ complexity even during leader failures, while maintaining the desirable low latency. This makes IBFT a highly efficient and resilient consensus algorithm, proving its value in frameworks like Hyperledger Besu. Ultimately, IBFT stands as a testament to the continuous evolution of BFT protocols, offering a practical, secure, and performant solution for decentralized systems where trust and consistency are paramount.

Sources

• M. Castro, B. Liskov, et al. Practical byzantine fault tolerance. In OsDI, volume 99, pages 173–186, 1999.
• R. Saltini and D. Hyland-Wood. IBFT 2.0: A safe and live variation of the IBFT blockchain consensus protocol for eventually synchronous networks. CoRR, abs/1909.10194, 2019
• H. Moniz. The Istanbul BFT Consensus Algorithm. arXiv preprint arXiv:2002.03613, 2020

Lais Ziegler

Dev in training... 👋

LinkedIn